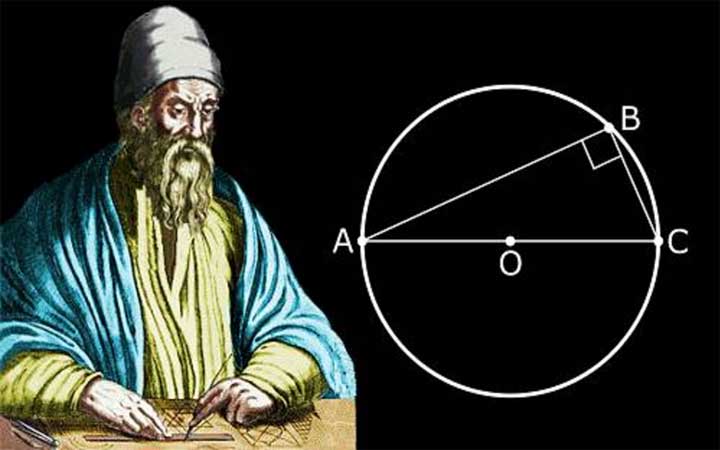
ศาสตราจารย์คณิตศาสตร์ยุคโบราณ

ยุคลิด เป็นชาวกรีก มีชีวิตอยู่ในราว 325 – 270 ปีก่อนคริสต์ศักราช เชื่อกันว่ายุคลิดเข้าเรียนที่โรงเรียนของเพลโตที่กรุงเอเธนส์ในอาณาจักรกรีกโบราณ ก่อนจะไปทำงานสร้างผลงานและชื่อเสียงที่เมืองอเล็กซานเดรีย จึงถูกเรียกว่ายุคลิดแห่งอเล็กซานเดรีย (Euclid of Alexandria) พระเจ้าอเล็กซานเดอร์มหาราชสร้างเมืองอเล็กซานเดรียตรงบริเวณเหนือสุดของอียิปต์เมื่อราว 330 ปีก่อนคริสต์ศักราช ต่อมาผู้ปกครองอียิปต์ได้สร้างสถาบันการศึกษายิ่งใหญ่ที่ถือกันว่าเป็นมหาวิทยาลัยแห่งแรกของโลกขึ้นที่เมืองนี้เรียกว่า The Musaeum ซึ่งมีหอสมุดที่ใหญ่ที่สุดของโลกยุคโบราณเรียกว่า Library of Alexandria ดึงดูดให้นักวิชาการเก่งๆให้มาศึกษาวิจัยและสอนหนังสือที่สถาบันแห่งนี้แบบเดียวกับยุคลิด
ผลงานสำคัญของยุคลิดคือการเขียนตำราทางคณิตศาสตร์และฟิสิกส์ที่มีอย่างน้อยที่สุด 9 ชิ้น แต่คงเหลืออยู่ในปัจจุบัน 6 ชิ้น คือ Elements, Data, On Divisions of Figures, Catoptrics, Phacnomena 5 เล่มนี้เป็นตำราคณิตศาสตร์ในหลากหลายสาขา และ Optics ซึ่งเป็นตำราฟิสิกส์เรื่องแสงและการมองเห็น หนังสือ Elements ของยุคลิดเป็นตำราทางเรขาคณิตและคณิตศาสตร์ที่มีชื่อเสียงที่สุด ได้รับการยกย่องเป็นตำราที่สำคัญที่สุดเล่มหนึ่งในประวัติศาสตร์ของโลก มีคนอ่านมากที่สุดเป็นอันดับสองรองจากคัมภีร์ไบเบิ้ล
Elements ตำราของมวลมนุษยชาติ

ยุคลิดรวบรวมความรู้ด้านคณิตศาสตร์ที่เขาเรียนรู้ทั้งหมดซึ่งส่วนใหญ่เป็นผลงานและทฤษฎีคณิตศาสตร์จากการค้นคว้าของนักคณิตศาสตร์รุ่นก่อนหน้าเขาจำนวน 4 คนได้แก่ Thales, Pythagoras, Hippocrates และ Eudoxus นำมาเรียบเรียงรวมเข้าด้วยกันอย่างมีระบบและเป็นลำดับเหตุผลต่อเนื่องกัน พร้อมทั้งเพิ่มเติมผลงานการคิดค้นของตัวเองให้มีความสมบูรณ์ยิ่งขึ้น กลายเป็นหนังสือ Elements ซึ่งเป็นตำราของมวลมนุษยชาติที่ถูกใช้เพื่อเรียนรู้คณิตศาสตร์อย่างยาวนานตั้งแต่สมัยกรีกจนถึงศตวรรษที่ 20 หนังสือ Elements มีทั้งหมด 13 เล่มแบ่งตามเนื้อหาเป็น 3 กลุ่มได้แก่
กลุ่มที่ 1 เล่มที่ 1 – 6 มีเนื้อหาเกี่ยวกับเรขาคณิตระนาบหรือเรขาคณิต 2 มิติ
กลุ่มที่ 2 เล่มที่ 7 – 10 มีเนื้อหาเกี่ยวกับทฤษฎีจำนวน
กลุ่มที่ 3 เล่มที่ 11 – 13 มีเนื้อหาเกี่ยวกับรูปทรงเรขาคณิต 3 มิติ
ว่ากันว่าในทันทีที่หนังสือ Elements ออกมายุคลิดก็ได้รับการชื่นชมอย่างกว้างขวาง หนังสือเล่มนี้ได้รับความนิยมแพร่หลายไปทั่วโลก อาจกล่าวได้ว่าไม่มีหนังสือเล่มใดที่มีอิทธิพลต่อวิถีชีวิตของมนุษย์และถูกใช้อย่างกว้างขวางเท่ากับ Elements หนังสือเล่มนี้ยังเป็นผลงานชิ้นเอกในการใช้ตรรกะกับคณิตศาสตร์ นักวิทยาศาสตร์เอกของโลกจำนวนมากรวมทั้ง Galileo Galilei, Isaac Newton และ Albert Einstein ต่างได้รับอิทธิพลจากหนังสือ Elements ทั้งสิ้น
เรขาคณิตที่ยืนยงกว่าสองสหัสวรรษ
สิ่งที่โดดเด่นที่สุดในหนังสือ Elements คือส่วนที่เกี่ยวกับเรขาคณิตซึ่งถือว่าเป็นต้นแบบของระบบคณิตศาสตร์ในปัจจุบัน ยุคลิดเริ่มต้นวิชาเรขาคณิตด้วยการกำหนดข้อตกลง 10 ประการ เขาเรียกข้อตกลง 5 ประการแรกว่าสิ่งที่เห็นจริงแล้ว (Axioms หรือ Common Notions) ซึ่งหมายถึงสิ่งที่เห็นได้จริงโดยไม่ต้องมีการพิสูจน์ในทางคณิตศาสตร์ ส่วนข้อตกลง 5 ประการหลังเรียกว่าสัจพจน์ (Postulates) หมายถึงสิ่งที่เห็นได้จริงโดยไม่ต้องพิสูจน์ในทางเรขาคณิต ข้อตกลงดังกล่าวมีดังนี้
Axioms
A1 สิ่งที่เท่ากับสิ่งเดียวกันย่อมเท่ากัน
A2 สิ่งที่เท่ากันเมื่อเพิ่มด้วยสิ่งที่เท่ากัน ผลย่อมเท่ากัน
A3 สิ่งที่เท่ากันเมื่อหักออกด้วยสิ่งที่เท่ากัน ผลย่อมเท่ากัน
A4 สิ่งที่เหมือนกับสิ่งอื่นทุกอย่างย่อมเท่ากับสิ่งนั้น
A5 ส่วนรวมย่อมใหญ่กว่าส่วนย่อย
Postulates
P1 สามารถลากเส้นตรงจากจุดหนึ่งไปยังอีกจุดหนึ่งได้
P2 สามารถต่อเส้นตรงที่มีความยาวจำกัดออกไปได้เรื่อยๆ
P3 สามารถสร้างวงกลมได้เมื่อกำหนดจุดศูนย์กลางและระยะทางใดๆ
P4 มุมฉากทุกมุมย่อมเท่ากัน
P5 ถ้าเส้นตรงเส้นหนึ่งตัดผ่านเส้นตรงอีกสองเส้นแล้วทําให้มุมภายในที่อยู่ข้างเดียวกันของเส้นตัดรวมกันน้อยกว่า 2 มุมฉาก ถ้าต่อเส้นตรงทั้งสองออกไปเรื่อยๆเส้นตรงทั้งสองจะตัดกันทางด้านที่มีมุมรวมกันน้อยกว่า 2 มุมฉาก
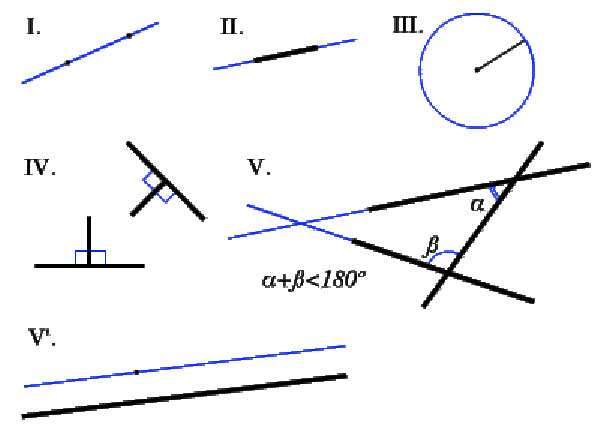
จากข้อตกลงทั้ง 10 ประการนี้ ยุคลิดสามารถนำไปสร้างทฤษฎีบทที่มีความซับซ้อนมากขึ้นเป็นลำดับได้ถึง 465 ทฤษฎี แล้วทำการพิสูจน์โดยใช้เหตุผลเชิงคณิตศาสตร์ที่ถูกต้องสวยงามว่าทฤษฎีบทเหล่านั้นเป็นจริง ทฤษฎีของนักคณิตศาสตร์ยุคก่อนหน้ายุคลิดได้ถูกรวบรวมเอาไว้ด้วย เช่น ทฤษฎีบทที่ 29 เรื่องสามเหลี่ยมมุมฉากของ Pythagoras เป็นต้น นอกจากนี้ยุคลิดยังให้นิยามคำศัพท์ทุกคำที่ใช้ในหนังสือ Elements ไว้อย่างชัดเจน เช่นคำว่า จุด เส้น ระนาบ เป็นต้น ด้วยมาตรฐานการเรียนรู้เรขาคณิตที่ยุคลิดได้วางไว้อย่างเป็นระบบในหนังสือ Elements นี้มันจึงถูกใช้ในการสอนวิชาเรขาคณิตในสถาบันการศึกษาทั่วโลกอย่างยาวนานกว่า 2,300 ปี
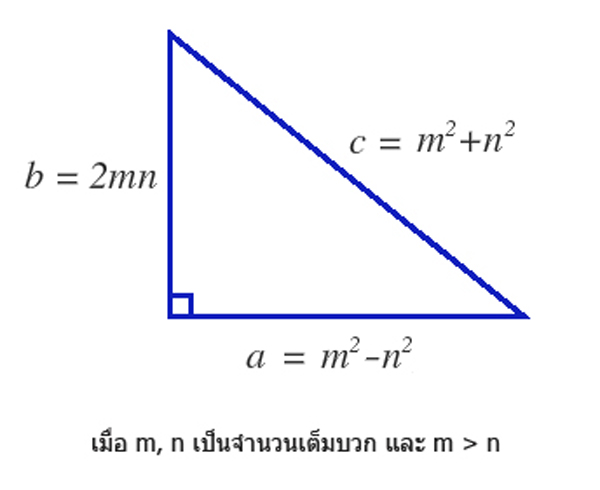
หนึ่งในผลงานที่ยอดเยี่ยมของยุคลิดได้แก่สูตรการหาความยาวทั้ง 3 ด้านของสามเหลี่ยมมุมฉากที่เรียกว่า Euclid’s formula ซึ่งใช้สำหรับหาตัวเลข 3 ตัวที่สอดคล้องกับทฤษฎีสามเหลี่ยมมุมฉากของพีทาโกรัสที่เรียกว่า Pythagorean triples ได้อย่างง่ายดายและมีประสิทธิภาพมาก ดังแสดงในรูปด้านล่าง
วางรากฐานทฤษฎีจำนวนยุคแรกเริ่ม

แน่นอนว่าวิชาเรขาคณิตคือผลงานชิ้นเอกของยุคลิดที่ใครๆก็รู้จักและให้การยกย่อง แต่เขายังมีผลงานด้านทฤษฎีจำนวนที่สำคัญมิใช่น้อย ถือเป็นการวางรากฐานในเรื่องทฤษฎีจำนวนในยุคแรกเริ่มไว้ให้นักคณิตศาสตร์ยุคต่อมาได้พัฒนาต่อยอดไปได้อย่างกว้างขวาง ในหนังสือ Elements ยุคลิดเขียนเกี่ยวกับทฤษฎีจำนวนไว้หลายที่โดยเฉพาะในเล่มที่ 7 – 10 ตัวอย่างผลงานเรื่องทฤษฎีจำนวนของยุคลิดที่น่าสนใจได้แก่
1. จำนวนเฉพาะ (Prime Number) – ยุคลิดเป็นคนแรกที่พิสูจน์ว่าจำนวนเฉพาะมีอยู่อย่างไม่จำกัดหรือมีจำนวนเป็นอนันต์ในทฤษฎีที่เรียกกันว่า Euclid’s theorem จำนวนเฉพาะหมายถึงจำนวนที่มีตัวประกอบ (หรือจำนวนที่หารมันลงตัว) 2 ตัว ได้แก่ 2, 3, 5, 7, 11, 13, … (1 ไม่ใช่เพราะมีตัวประกอบตัวเดียว) วิธีพิสูจน์ของยุคลิดก็น่าสนใจมาก เขาพิสูจน์ว่าเมื่อพิจารณาเซ็ตของจำนวนเฉพาะที่มีจำนวนจำกัดใดๆ ถ้านำผลคูณของจำนวนเฉพาะในเซ็ตทั้งหมดบวกด้วย 1 จะได้จำนวนเฉพาะตัวใหม่ ซึ่งหมายถึงว่าจำนวนเฉพาะสามารถมีได้อย่างไม่จำกัด
2. จำนวนสมบูรณ์ (Perfect Number) – จำนวนสมบูรณ์หมายถึงจำนวนที่มีค่าเท่ากับผลบวกของตัวประกอบ (จำนวนที่หารมันลงตัว) ทั้งหมดของมันยกเว้นตัวมันเอง เช่น 6 มีตัวประกอบคือ 1, 2 และ 3 (ยกเว้นตัวมันเอง) และ 1+2+3 = 6 ดังนั้น 6 จึงเป็นจำนวนสมบูรณ์ จำนวนสมบูรณ์ 4 ตัวแรกได้แก่
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
8,128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1,016 + 2,032 + 4,064
นักคณิตศาสตร์ศึกษาเกี่ยวกับจำนวนสมบูรณ์มาตั้งแต่ก่อนยุคของยุคลิด แต่ยุคลิดเป็นผู้คิดค้นสูตรในการหาจำนวนสมบูรณ์สำเร็จเป็นคนแรก สูตรจำนวนสมบูรณ์ของยุคลิดคือ
2n-1(2n − 1) เป็นจำนวนสมบูรณ์ เมื่อ 2n − 1 เป็นจำนวนเฉพาะ
สำหรับ n = 2; 2n − 1= 3 ; 21(22 − 1) = 6
สำหรับ n = 3; 2n − 1= 7 ; 22(23 − 1) = 28
สำหรับ n = 5; 2n − 1= 31 ; 24(25 − 1) = 496
สำหรับ n = 7; 2n − 1= 127 ; 26(27 − 1) = 8128
หลังจากยุคลิดคิดสูตรนี้ไว้นาน 2,000 ปี Leonhard Euler จึงได้พิสูจน์ว่าจำนวนสมบูรณ์ทั้งหมดเป็นไปตามสูตรหรือรูปแบบของยุคลิดซึ่งเรียกกันว่าทฤษฎี Euclid–Euler theorem นอกจากนี้ยุคลิดยังค้นพบว่าจำนวนสมบูรณ์ยังมีคุณสมบัติที่น่าสนใจอีกหลายอย่าง เช่น มันมีค่าเท่ากับผลบวกของจำนวนเต็มต่อเนื่องจนถึงตัวประกอบที่เป็นจำนวนเฉพาะที่มีค่ามากที่สุด
6 = 1 + 2 + 3
28 = 1 + 2 + 3 + 4 + 5 + 6 + 7
496 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + … + 30 + 31
8,128 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + … + 126 + 127
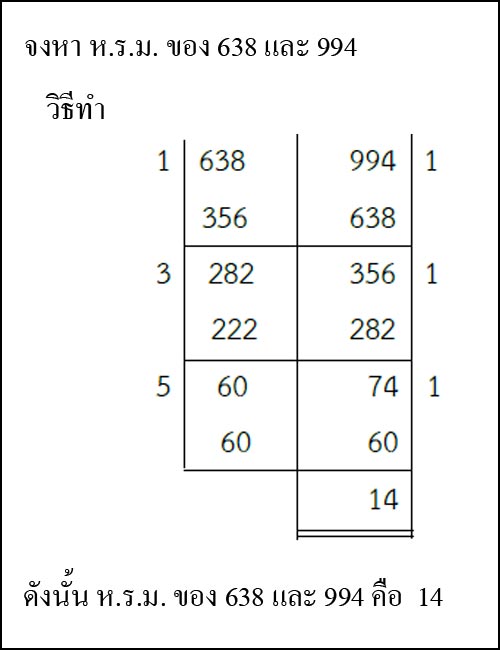
3. ตัวหารร่วมมาก (ห.ร.ม.) – ห.ร.ม. ของจำนวนเต็มสองจำนวนคือจำนวนเต็มที่มากที่สุดที่หารทั้งสองจำนวนลงตัว เราสามารถหา ห.ร.ม. ได้หลายวิธี วิธีพื้นฐานคือให้แยกตัวประกอบของทั้งสองจำนวนแล้วนำตัวประกอบที่ซ้ำกันของทั้งสองจำนวนทุกตัวมาคูณกันจะได้เป็น ห.ร.ม. แต่วิธีนี้จะทำได้สำหรับจำนวนที่มีค่าน้อยๆเท่านั้น หากเป็นจำนวนที่มีค่าจำนวนมากๆการแยกตัวประกอบจะยุ่งยากและมีจำนวนตัวประกอบมากเกินไป ยุคลิดได้คิดค้นวิธีหา ห.ร.ม. ที่มีประสิทธิภาพมากและใช้ได้กับทุกจำนวนเรียกว่าขั้นตอนวิธีแบบยุคลิด (Euclidean Algorithm) วิธีการก็ไม่ซับซ้อนเริ่มจากใช้จำนวนที่มีค่าน้อยกว่าเป็นตัวหารนำไปหารจำนวนที่มีค่ามากกว่า เหลือเศษเท่าไรใช้เศษนั้นเป็นตัวหารนำไปหารตัวหารก่อนหน้า ทำไปเรื่อยๆจนกว่าจะหารลงตัว ตัวหารที่ทำให้การหารลงตัวคือ ห.ร.ม. รูปด้านล่างแสดงวิธีหา ห.ร.ม. ของ 638 และ 994 ขั้นตอนวิธีแบบยุคลิด ส่วน ค.ร.น. ก็สามารถหาได้จากผลคูณของจำนวนทั้งสองหารด้วย ห.ร.ม.
ผลงานเด่นทั้งคณิตศาสตร์และฟิสิกส์

นอกจากคณิตศาสตร์ที่เป็นผลงานหลักแล้วยุคลิดยังมีผลงานด้านฟิสิกส์อีกด้วย หนังสือ Optics ของเขาเป็นหนังสือที่มีอิทธิพลอย่างมากในเรื่องแสงและการมองเห็น ยุคลิดได้อธิบายพฤติกรรมของแสงโดยการใช้เรขาคณิตที่เขาได้พัฒนาขึ้นในหนังสือ Elements ทฤษฎีแสงของยุคลิดเป็นพื้นฐานสำคัญในการเขียนภาพ Perspective, วิธีการทางดาราศาสตร์ และการเดินเรือมาเป็นเวลานานกว่า 2,000 ปี แม้ว่าในสมัยของยุคลิดยังมีการเข้าใจผิดว่าการมองเห็นวัตถุเกิดจากดวงตาปล่อยแสงไปยังวัตถุ ต่างกับในปัจจุบันที่ชัดเจนแล้วว่าเกิดจากแสงตกกระทบวัตถุแล้วเกิดการสะท้อนเข้าสู่ดวงตาของเรา แต่ทฤษฎีแสงของยุคลิดใช้ได้ผลดีสมบูรณ์แบบเพราะว่ามันเป็นเรขาคณิต ไม่ว่าแสงจะเดินทางเข้าสู่ดวงตาหรือออกจากดวงตาก็ให้ผลเหมือนกัน
นอกจากนี้ยุคลิดยังมีผลงานด้านกลศาสตร์อีกหลายอย่าง เช่น การเคลื่อนที่ของวัตถุ, แนวคิดเกี่ยวกับแรงโน้มถ่วง และทฤษฎีเกี่ยวกับคานงัด ยุคลิดเขียนหนังสือเกี่ยวกับกลศาสตร์ไว้หลายเล่มเพียงแต่ไม่มีเล่มใดเหลือรอดมาถึงปัจจุบันเลย
บิดาแห่งเรขาคณิตที่ทั่วโลกยกย่อง

ยุคลิดเป็นนักคณิตศาสตร์ที่มีผลงานยอดเยี่ยมในหลากหลายสาขา โดยเฉพาะอย่างยิ่งในวิชาเรขาคณิตที่เขาได้พัฒนาขึ้นและวางระบบการเรียนรู้ที่เป็นมาตรฐานจนเป็นต้นแบบของระบบคณิตศาสตร์ในปัจจุบัน รวมทั้งเขายังได้ใช้ความเชี่ยวชาญอันเอกอุด้านเรขาคณิตไปพัฒนาทฤษฎีแสงซึ่งเป็นพื้นฐานสำคัญและมีประโยชน์ต่อการใช้งานในหลายสาขา ยุคลิดจึงได้รับการยกย่องเป็นบิดาแห่งเรขาคณิต

ข้อมูลและภาพจาก famousscientists, wikipedia, storyofmathematics