1. เลออนฮาร์ด ออยเลอร์ (Leonhard Euler)
เลออนฮาร์ด ออยเลอร์ (ค.ศ. 1707 – 1783) เป็นนักคณิตศาสตร์และนักฟิสิกส์ชาวสวิส ผู้ซึ่งมีผลงานการคิดค้นที่สำคัญทางคณิตศาสตร์ในหลายสาขา เช่น แคลคูลัสและทฤษฎีกราฟ และยังเป็นผู้ริเริ่มพัฒนาในอีกหลายสาขาของคณิตศาสตร์ ได้แก่ โทโปโลยีและทฤษฎีจำนวนเชิงวิเคราะห์ เป็นต้น เป็นคนแรกที่นำแคลคูลัสเข้าไปประยุกต์ในวิชาฟิสิกส์ และเป็นคนแรกที่ใช้คำว่า “ฟังก์ชัน” ในการบรรยายถึงความสัมพันธ์ที่เกี่ยวข้องกับตัวแปร เช่น y = f(x) รวมทั้งยังเป็นผู้คิดค้นสัญลักษณ์สำคัญในทางคณิตศาสตร์อีกหลายอย่างซึ่งยังคงใช้จนถึงปัจจุบัน นอกจากนี้เขายังมีผลงานด้านฟิสิกส์ ดาราศาสตร์ ตรรกศาสตร์และดนตรีอีกด้วย
ออยเลอร์ฉายแววความเป็นอัจฉริยะทางคณิตศาสตร์ตั้งแต่เด็ก หลังเรียนจบได้ทำงานเป็นอาจารย์สอนคณิตศาสตร์ที่เซนต์ปีเตอร์สเบิร์ก 14 ปี จึงย้ายไปสอนที่เบอร์ลิน 25 ปี แล้วกลับมาสอนที่เซนต์ปีเตอร์สเบิร์กจวบจนวาระสุดท้ายของชีวิต ออยเลอร์เป็นหนึ่งในนักคณิตศาสตร์ที่มีผลงานมากที่สุดในโลก ผลงานที่เขาเขียนมีมากถึง 30,000 หน้า รวบรวมเป็นหนังสือได้ถึง 75 เล่ม ออยเลอร์ตาบอดสนิทตลอด 17 ปีสุดท้ายในชีวิต แต่เป็นช่วงนี้เองที่เขาสามารถผลิตผลงานได้มากถึงครึ่งหนึ่งของผลงานทั้งหมด ออยเลอร์ได้รับการยกย่องว่าเป็นนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดคนหนึ่งของโลก
ผลงานเด่น :
– ริเริ่มวิชาโทโปโลยีและทฤษฎีกราฟ
– คิดค้นทฤษฏีจำนวนเชิงวิเคราะห์
– เป็นคนแรกที่ประยุกต์แคลคูลัสเข้าไปยังวิชาฟิสิกส์
– เป็นคนแรกที่ใช้ฟังก์ชัน f(x) บรรยายถึงความสัมพันธ์ที่เกี่ยวข้องกับตัวแปร
– คิดค้นและริเริ่มใช้สัญลักษณ์สำคัญทางคณิตศาสตร์ ได้แก่ e แทนลอการิทึมธรรมชาติ, Σ แทนผลรวม, i แทนหน่วยจินตภาพ และยังเป็นผู้นำสัญลักษณ์ π (pi) มาใช้แทนอัตราส่วนเส้นรอบวงต่อเส้นผ่าศูนย์กลางของวงกลมจนได้รับความนิยม
สูตรเด็ด :
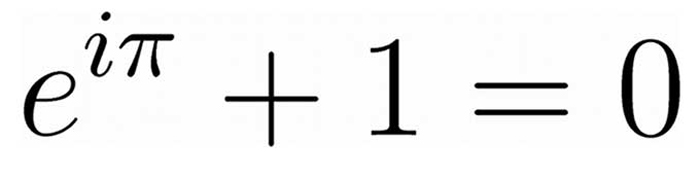
→ เรียกว่าเอกลักษณ์ของออยเลอร์ (Euler’s identity) ซึ่งเป็นกรณีพิเศษของสูตรออยเลอร์ (Euler’s formula) เป็นสูตรคณิตศาสตร์ที่โดดเด่นมากเนื่องจากใช้ทั้งเครื่องหมายบวก คูณ ยกกำลัง และเท่ากับเพียงครั้งเดียว และยังใช้ค่าคงที่สำคัญถึง 5 ตัวคือ 0, 1, e, i และ π ได้รับการโหวตให้เป็น “สูตรคณิตศาสตร์ที่งดงามที่สุดเท่าที่เคยมีมา” เมื่อปี 1988

2. โยฮันน์ คาร์ล ฟรีดริช เกาส์ (Johann Carl Friedrich Gauss)
ฟรีดริช เกาส์ (ค.ศ. 1777 – 1855) นักคณิตศาสตร์ชาวเยอรมัน เจ้าของฉายา “เจ้าชายแห่งคณิตศาสตร์” (Prince of Mathematics) ผู้มีผลงานโดดเด่นในหลากหลายสาขา ได้แก่ ทฤษฎีจำนวน, พีชคณิต, สถิติ, คณิตวิเคราะห์, เรขาคณิต, ทฤษฎีเมตริก, ยีออเดซี, ธรณีฟิสิกส์, กลศาสตร์, ไฟฟ้าสถิต และดาราศาสตร์ เกาส์เป็นอัจฉริยบุคคลระดับเดียวกับไอน์ไสตน์ ไม่ว่าเขาจะจับเรื่องใดก็จะพบความรู้ที่สำคัญและพบวิธีคำนวณใหม่ซึ่งเป็นรากฐานของวิชานั้นอยู่เสมอ นักคณิตศาสตร์รุ่นหลังต่างก็ยอมรับว่ามีเกาส์อยู่ทุกที่ในวิชาคณิตศาสตร์ “Gauss lives everywhere in mathematics”
ตอนเกาส์อายุ 7 ขวบเขาใช้เวลาไม่กี่วินาทีตอบโจทย์การบวกเลขตั้งแต่ 1 ถึง 100 ในห้องเรียนจนคุณครูตะลึง ยิ่งเมื่อทราบวิธีคิดยิ่งทึ่งมาก อายุ 19 ปีค้นพบวิธีการสร้างรูป 17 เหลี่ยมด้านเท่าโดยใช้วงเวียนและไม้บรรทัดเท่านั้น ซึ่งยุคลิดได้เคยแสดงการสร้างรูป 3, 4, 5 และ 15 เหลี่ยมด้านเท่าโดยใช้ไม้บรรทัดและวงเวียน แล้วหลังจากนั้นอีก 2,000 ปี ยังไม่มีใครทำได้เพิ่มอีกเลย อายุ 21 ปีค้นพบทฤษฎีจำนวน อายุ 23 ปีค้นพบวิธีการคำนวณที่เรียกว่า “วิธีกำลังสองน้อยที่สุด” ซึ่งเป็นรากฐานสำคัญของทฤษฎีการประมาณค่าที่เรายังใช้กันอยู่ในปัจจุบัน นำไปใช้คำนวณวิถีวงโคจรดาวเคราะห์น้อยซีรีสจากข้อมูลที่มีเพียงน้อยนิดสำเร็จ เกาส์ยังมีผลงานอีกมากมายในหลากหลายสาขาวิชา เขาได้รับการยกย่องว่าเป็นนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดนับจากยุคโบราณ
ผลงานเด่น :
– คิดค้นทฤษฎีจำนวนสมัยใหม่
– เป็นผู้แรกที่สามารถพิสูจน์ทฤษฎีบทมูลฐานของพีชคณิตซึ่งเป็นวิทยานิพนธ์ปริญญาเอกของเขา
– คิดค้นวิธีกำลังสองน้อยที่สุด
– พัฒนาเรขาคณิตนอกระบบยุคลิด
– ค้นพบทฤษฎีของฟังก์ชันเชิงวงรี
สูตรเด็ด :
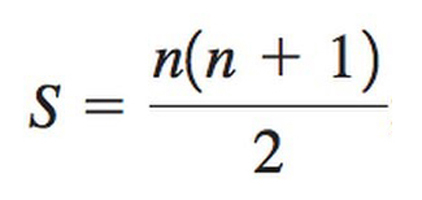
→ เป็นสูตรใช้คำนวณผลบวกจำนวนนับ n จำนวน เช่น 1 + 2 + 3 + 4 + … + 98 + 99 + 100 = 100 (100+1)/2 = 5050 ซึ่งมาจากเทคนิคที่เขาใช้ตอบโจทย์ในห้องเรียนตอนยังเด็กจนทำให้คุณครูทึ่งอย่างมาก

3. ไอแซก นิวตัน (Isaac Newton)
ไอแซก นิวตัน (ค.ศ. 1642 – 1727) นักคณิตศาสตร์ นักฟิสิกส์ และนักดาราศาสตร์ชาวอังกฤษผู้ซึ่งเป็นที่ยอมรับอย่างกว้างขวางว่าเป็นหนึ่งในนักวิทยาศาสตร์ที่มีอิทธิพลมากที่สุดตลอดกาลและมีบทบาทสำคัญในการปฏิวัติทางวิทยาศาสตร์ นิวตันมีผลงานด้านฟิสิกส์และดาราศาสตร์ที่สำคัญมากมายโดยเฉพาะอย่างยิ่งการคิดค้นกฎการเคลื่อนที่และกฎแรงโน้มถ่วงซึ่งเป็นกฎทางวิทยาศาสตร์ที่เป็นเสาหลักของการศึกษาจักรวาลทางกายภาพตลอดมา ทำให้นิวตันได้รับการยกย่องให้เป็นหนึ่งในนักวิทยาศาสตร์ผู้ยิ่งใหญ่ของโลก แต่ผลงานด้านคณิตศาสตร์ของเขาก็โดดเด่นไม่แพ้กัน
นิวตันได้รับการยกย่องว่าเป็นผู้คิดค้นและพัฒนาแคลคูลัสเชิงปริพันธ์และอนุพันธ์ ร่วมกับกอทท์ฟรีด ไลบ์นิซนักคณิตศาสตร์คนสำคัญชาวเยอรมัน นิวตันเป็นผู้คิดค้นทฤษฎีบททวินามที่ใช้ได้สำหรับเลขยกกำลังใดๆ เขาเป็นผู้ค้นพบ Newton’s identities, Newton’s method, เส้นโค้งบนระนาบลูกบาศก์ (โพลีโนเมียลอันดับสามของตัวแปรสองตัว) เขามีส่วนอย่างสำคัญต่อทฤษฎี finite differences และเป็นคนแรกที่ใช้เศษส่วนเลขชี้กำลัง (fractional indices) และนำเรขาคณิตเชิงพิกัดมาใช้หาคำตอบจากสมการไดโอแฟนทีน เขาหาค่าผลบวกย่อยโดยประมาณของอนุกรมฮาร์โมนิกได้โดยใช้ลอการิทึม (ก่อนจะมีสมการผลรวมของออยเลอร์) และเป็นคนแรกที่ใช้อนุกรมกำลัง กล่าวกันว่าผลงานของนิวตันเป็นความก้าวหน้าอันยิ่งใหญ่ในทุกสาขาของคณิตศาสตร์ในยุคนั้น
ผลงานเด่น :
– คิดค้นวิชาแคลคูลัส
– คิดค้นทฤษฎีบททวินาม
– ค้นพบวิธีการกระจายอนุกรม
– ผู้ค้นพบ Newton’s identities,Newton’s method
– เป็นคนแรกที่ใช้เศษส่วนเลขชี้กำลัง (fractional indices) และนำเรขาคณิตเชิงพิกัดมาใช้หาคำตอบจากสมการไดโอแฟนทีน
สูตรเด็ด :
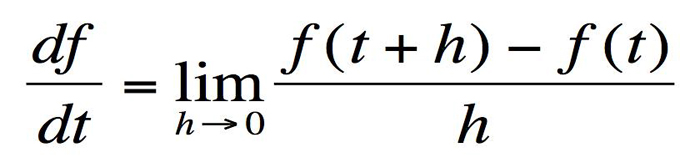
→ เป็นสูตรที่ใช้หาอัตราการเปลี่ยนแปลงขณะใดขณะหนึ่งของฟังชั่นซึ่งเป็นพื้นฐานของวิชาแคลคูลัสที่นิวตันคิดค้นขึ้นเพื่อใช้พัฒนากฎการเคลื่อนที่และกฎแรงโน้มถ่วง สูตรนี้เองที่พลิกโฉมและทำให้วิทยาศาสตร์ก้าวหน้าขึ้นอย่างมาก

ยุคลิดแห่งอเล็กซานเดรีย (325 – 270 ปีก่อนคริสต์ศักราช) เป็นนักคณิตศาสตร์ที่มีอิทธิพลมากที่สุดจนกระทั่งถึงศตวรรษที่ 20 เป็นศาสตราจารย์ด้านคณิตศาสตร์ของมหาวิทยาลัยอเล็กซานเดรียยุคกรีกโบราณต่อจากเพลโตและก่อนหน้าอาร์คีมีดีส ผลงานที่สำคัญของยุคลิดคือการเขียนตำราทางคณิตศาสตร์และดาราศาสตร์ที่มีอย่างน้อยที่สุด 9 ชิ้น แต่คงเหลืออยู่ในปัจจุบัน 5 ชิ้น คือ Division of Figures, Data และ Phacnomena ที่เป็นตำราเรขาคณิต, Optics เป็นตำราเกี่ยวกับปรากฏการณ์ของแสง และ Elements ตำราทางเรขาคณิตและคณิตศาสตร์ที่มีชื่อเสียงที่สุด
หนังสือ Elements เป็นตำราที่สำคัญที่สุดเล่มหนึ่งในประวัติศาสตร์ของมวลมนุษยชาติ มีคนอ่านมากที่สุดเป็นดับสองรองจากคำภีร์ไบเบิ้ล ถือว่าเป็นต้นแบบของระบบคณิตศาสตร์ในปัจจุบัน หนังสือ Elements มีทั้งหมด 13 เล่ม ซึ่งมีเนื้อหาส่วนใหญ่เป็นทฤษฏีบทเรขาคณิต แต่ก็มีการกล่าวถึงพีชคณิต เรขาคณิตเชิงพีชคณิตเบื้องต้น และทฤษฎีจำนวนเบื้องต้น เนื้อหาส่วนใหญ่เป็นผลงานของนักคณิตศาสตร์รุ่นก่อนที่ได้คิดค้นเอาไว้ เช่น พีทาโกรัสและยูโดซุส แต่ยุคลิดนำมารวบรวมเข้าด้วยกันอย่างมีระบบและเป็นลำดับเหตุผลต่อเนื่องกัน แม้ว่ายุคลิดจะไม่ได้เป็นนักคณิตศาสตร์ที่สร้างสรรค์งานขึ้นใหม่ แต่ผลงานที่เขารวบรวมขึ้นอย่างเป็นระบบกลับมีผลกระทบต่อมนุษยชาติมามากกว่า 2,300 ปี โดยเฉพาะทางด้านเรขาคณิต ยุคลิดจึงได้รับการยกย่องให้เป็นบิดาแห่งวิชาเรขาคณิต
ผลงานเด่น :
– หนังสือ Elements ที่เป็นต้นแบบของระบบคณิตศาสตร์ในปัจจุบัน
– หนังสือตำราเรขาคณิต Division of Figures, Data และ Phacnomena
สูตรเด็ด :
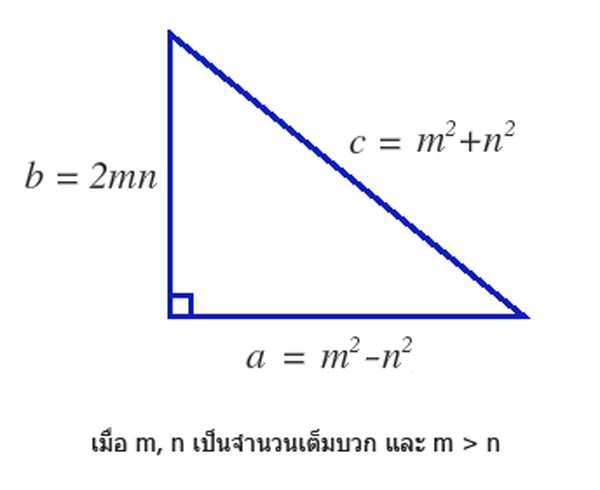
→ เรียกว่า Euclid’s formula เป็นสูตรที่ใช้หาความยาวทั้ง 3 ด้านของสามเหลี่ยมมุมฉากหรือตัวเลข 3 ตัวที่สอดคล้องกับทฤษฎีสามเหลี่ยมมุมฉากของพีทาโกรัสที่เรียกว่า Pythagorean triples ได้อย่างง่ายดายและมีประสิทธิภาพมาก

อาร์คิมิดีส (287- 212 ก่อนคริสต์ศักราช) เป็นนักคณิตศาสตร์ นักดาราศาสตร์ นักปรัชญา นักฟิสิกส์ และวิศวกรชาวกรีก ได้รับการยกย่องว่าเป็นหนึ่งในบรรดานักวิทยาศาสตร์ผู้ยิ่งใหญ่ของโลกและเป็นนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดในยุคโบราณ อาร์คิมิดีสมีผลงานด้านวิทยาศาสตร์มากมาย เป็นผู้วางรากฐานให้แก่วิชาสถิตยศาสตร์, สถิตยศาสตร์ของไหล และกลศาสตร์ เป็นผู้คิดค้นนวัตกรรมเครื่องจักรกลหลายชิ้น รวมทั้งอุปกรณ์เครื่องผ่อนแรงที่ยังใช้งานอยู่จนถึงปัจจุบัน และมีผลงานด้านคณิตศาสตร์ที่สำคัญมากมายเช่นกัน
อาร์คิมิดีสมีงานเขียนหนังสือไว้หลายเล่มแต่ส่วนมากไม่สามารถรอดมาถึงปัจจุบัน ผลงานที่รอดมาได้อย่างเช่นหนังสือว่าด้วยด้วยดุลยภาพของระนาบที่ใช้คำนวณพื้นที่และจุดศูนย์กลางมวลของวัตถุรูปทรงต่างๆ หนังสือว่าด้วยการวัดวงกลมที่อาร์คิมิดีสแสดงให้เห็นว่าค่า π (pi) มีค่ามากกว่า 223/71 แต่น้อยกว่า 22/7 ซึ่งตัวเลขหลังนี้ถูกนำมาใช้เป็นค่าประมาณของ π มาตลอดจนถึงปัจจุบัน หนังสือวงก้นหอยอาร์คิมิดีสที่เกี่ยวกับเส้นโค้งที่เกิดจากจุดเคลื่อนที่ อาร์คิมิดีสเป็นผู้คิดค้นสูตรคณิตศาสตร์สำหรับคำนวณพื้นที่และปริมาตรของรูปทรงต่างๆ ทั้งทรงกลม ทรงกระบอก ทรงกรวย ภาคตัดกรวย รวมทั้งคิดค้นสมการหาปริมาตรของรูปทรงที่เกิดจากพื้นผิวที่ได้จากการหมุน ผลงานของอาร์คิมิดีสมีอิทธิพลต่อวงการคณิตศาสตร์อย่างมากตั้งแต่ยุคโบราณจนถึงปัจจุบัน
ผลงานเด่น :
– หนังสือว่าด้วยด้วยดุลยภาพของระนาบและการคำนวณจุดศูนย์กลางมวลของวัตถุ
– หนังสือว่าด้วยการวัดวงกลมและการประมาณค่า π (pi)
– คิดค้นสูตรคณิตศาสตร์สำหรับคำนวณพื้นที่และปริมาตรของรูปทรงต่างๆมากมาย
– คิดค้นสมการหาปริมาตรของรูปทรงที่เกิดจากพื้นผิวที่ได้จากการหมุน
สูตรเด็ด :
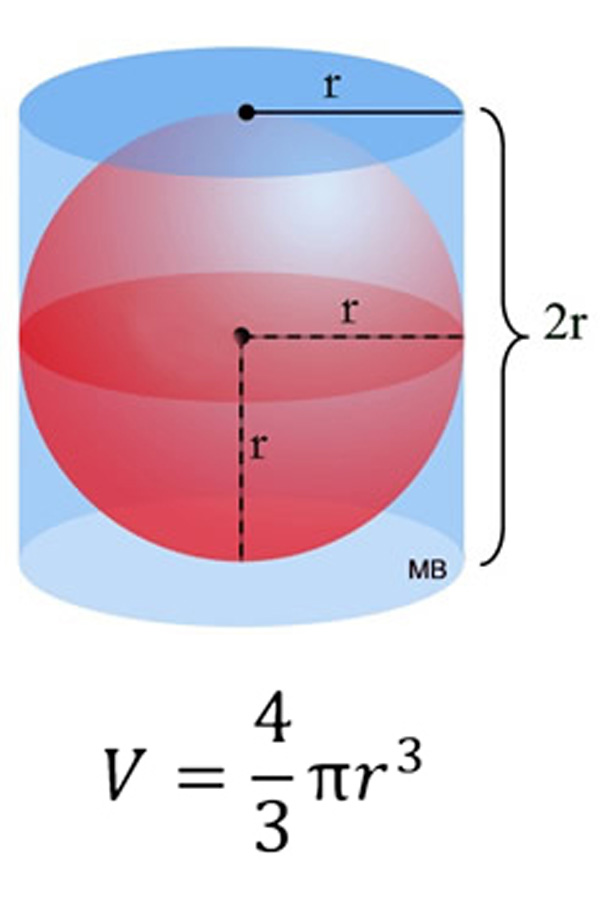
→ เป็นสูตรคํานวณปริมาตรทรงกลมที่อาร์คิมิดีสคิดค้นโดยอาศัยความสัมพันธ์ระหว่างทรงกลมกับทรงกระบอกที่มีความสูงและเส้นผ่านศูนย์กลางเท่ากัน ซึ่งอาร์คิมิดีสได้ค้นพบว่าทรงกลมจะมีปริมาตรเป็น 2/3 เท่าของปริมาตรทรงกระบอก และทรงกลมมีพื้นที่ผิวเป็น 2/3 เท่าของพื้นที่ผิวทรงกระบอกด้วย

พีทาโกรัส (570–495 ปีก่อนคริสต์ศักราช) เป็นนักคณิตศาสตร์และนักปราชญ์ชาวกรีกโบราณผู้ได้ชื่อว่าเป็น “บิดาแห่งตัวเลข” เป็นลูกศิษย์ของเทลีส (Thales) นักปราชญ์เอกคนแรกของโลก และเดินทางไปศึกษาในหลายประเทศ เช่น อียิปต์ บาบิโลน และอินเดีย แล้วกลับมาตั้งโรงเรียนที่บ้านเกิดสอนปรัชญา คณิตศาสตร์ และดาราศาสตร์ ใช้รูปดาวห้าแฉกเป็นสัญลักษณ์ มีลูกศิษย์มากมาย สาวกของพีทาโกรัสตั้งชมรม “พีทาโกเรียน” มีความเชื่อว่าคณิตศาสตร์เป็นพื้นฐานของทุกสิ่งทุกอย่าง ถ้าไม่มีคณิตศาสตร์แล้วทุกอย่างก็จะไม่เกิดขึ้น
พีทาโกรัสเป็นผู้คิดค้นสูตรคูณหรือตารางพีทาโกเรียน (Pythagorean Table) ที่ใช้งานมาจนถึงปัจจุบัน เขาเป็นผู้ค้นพบและสร้างทฤษฎีเรขาคณิตมากมาย โดยเฉพาะอย่างยิ่งทฤษฎีสามเหลี่ยมมุมฉากที่ว่า a² + b² = c² หรือทฤษฎีบทพีทาโกรัสอันโด่งดัง ซึ่งแม้ว่าชาวบาบิโลนจะมีความรู้ในเรื่องนี้มาก่อนหน้านับพันปีแต่เขาเป็นคนแรกที่พิสูจน์ทฤษฎีนี้ได้ พีทาโกรัสเป็นผู้พบว่าผลบวกมุมภายในของสามเหลี่ยมใดๆ จะเท่ากับ 2 มุมฉาก (180°) เสมอ รวมไปถึงค้นพบผลบวกของมุมภายในรูป n เหลี่ยม = (2n – 4) มุมฉาก และยังเป็นผู้ค้นพบตัวเลขอัศจรรย์มากมาย เช่น จำนวนสมบูรณ์และจำนวนแห่งมิตรภาพ พีทาโกรัสเป็นผู้คนพบว่าเรามองเห็นวัตถุได้เนื่องจากแสงสะท้อนจากวัตถุมากระทบกับตาเรา ค้นพบว่าเสียงเกิดจากการสั่นสะเทือนของวัตถุ นอกจากนี้เขายังเป็นคนแรกที่ตั้งทฤษฎีเกี่ยวกับโลกกลม และหมุนรอบตัวเองรวมถึงดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ก็หมุนรอบตัวเองเช่นกัน ซึ่งต่อมาได้รับการพิสูจน์ว่าถูกต้อง
ผลงานเด่น :
– สร้างสูตรคูณ
– สร้างทฤษฎีบทพีทาโกรัส
– ทฤษฎีคณิตศาสตร์มากมาย
– ทฤษฎีโลกกลมและหมุนรอบตัวเอง
สูตรเด็ด :
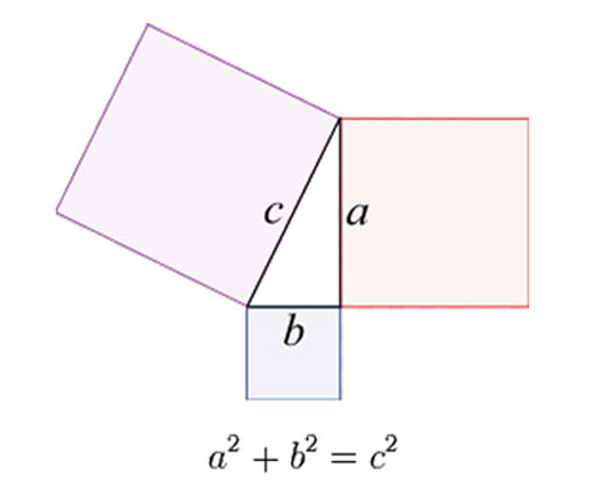
→ เป็นสูตรของทฤษฎีบทพีทาโกรัสที่ว่าผลรวมของค่ากำลังสองของความยาวด้านประกอบมุมฉากเท่ากับค่ากำลังสองของความยาวด้านตรงข้ามมุมฉาก หรือ a2 + b2 = c2 เป็นหนึ่งในสูตรคณิตศาสตร์ที่คนรู้จักกันมากที่สุด

7. เรอเน เดการ์ต (René Descartes)
เรอเน เดการ์ต (ค.ศ. 1596 – 1650) เป็นนักปรัชญาและนักคณิตศาสตร์ชาวฝรั่งเศสผู้คิดวิธีหาสัจจะในวิชาวิทยาศาสตร์และในชีวิตโดยเชื่อมั่นว่าตรรกะและวิธีพิสูจน์ของคณิตศาสตร์สามารถเชื่อมโยงและเป็นกุญแจไขความลึกลับต่างๆได้ เขาเป็นผู้ที่บุกเบิกปรัชญาสมัยใหม่ แนวคิดของเขามีผลต่อนักคิดร่วมสมัยไปจนถึงนักปรัชญารุ่นต่อมา เดการ์ตเป็นเจ้าของความคิดและวาทะอันโด่งดัง “เพราะฉันคิด ฉันจึงมีอยู่” (I think, therefore I am) ผลงานสุดยอดของเดการ์ตคือการสร้างวิชาเรขาคณิตวิเคราะห์ (Analytic Geometry) ซึ่งได้จากการรวมพีชคณิตกับเรขาคณิตเข้าด้วยกันทั้งๆที่ในอดีตนักคณิตศาสตร์ทั้งหลายเคยคิดว่าวิชาทั้งสองนี้ไม่เกี่ยวข้องกันเลย อันมีผลทำให้วิชาทั้งสองได้พัฒนาซึ่งกันและกันมาจนทุกวันนี้
มีตำนานเล่าว่าวันหนึ่งเดการ์ตเห็นแมลงวันบินวนไปมาในห้อง เขาพยายามจะระบุตำแหน่งของแมลงวันบนผนังห้องจึงได้จินตนาการว่าผนังห้องมีแกนสองแกนที่ตั้งฉากกัน จากนั้นตำแหน่งของแมลงวันก็สามารถระบุได้จากระยะทางที่มันอยู่ห่างจากแกนทั้งสอง ทำให้เกิดวิทยาการสาขาใหม่เป็นระบบการบอกตำแหน่งซึ่งมีแกนสองแกนตั้งฉากกัน จุดตัดของแกนทั้งสองเรียกจุดกำเนิด เดการ์ตได้แสดงให้เห็นว่าตำแหน่งของจุดทุกจุดบนระนาบ (เรียกระนาบคาร์ทีเซียน) สามารถระบุได้ด้วยตัวเลข 2 ค่าซึ่งบอกระยะทางของจุดนั้นในแนวนอนและแนวดิ่ง และเส้นตรง เส้นโค้ง วงรี วงกลม ไฮเปอร์โบลา พาราโบลา ฯลฯ สามารถแทนได้ด้วยสมการพีชคณิต ดังนั้นการแก้โจทย์เรขาคณิตก็อาจทำได้โดยการแก้โจทย์พีชคณิต ในเวลาต่อมาพิกัดคาร์ทีเซียนใน 2 มิติก็ได้รับการต่อยอดให้ครอบคลุมทั้ง 3 มิติ วิชาเรขาคณิตที่มีสมการพีชคณิตกำกับทำให้นักวิทยาศาสตร์สามารถวิเคราะห์การเคลื่อนที่ได้ทุกรูปแบบ เดการ์ตจึงได้รับการยกย่องให้เป็นบิดาของวิชาเรขาคณิตวิเคราะห์
ผลงานเด่น :
– สร้างวิชาเรขาคณิตวิเคราะห์
– วางรากฐานปรัชญากลุ่มเหตุผลนิยม (Rationalism) ซึ่งเป็นแนวคิดปรัชญาหลักในยุโรปสมัยศตวรรษที่ 17 และ 18
สูตรเด็ด :
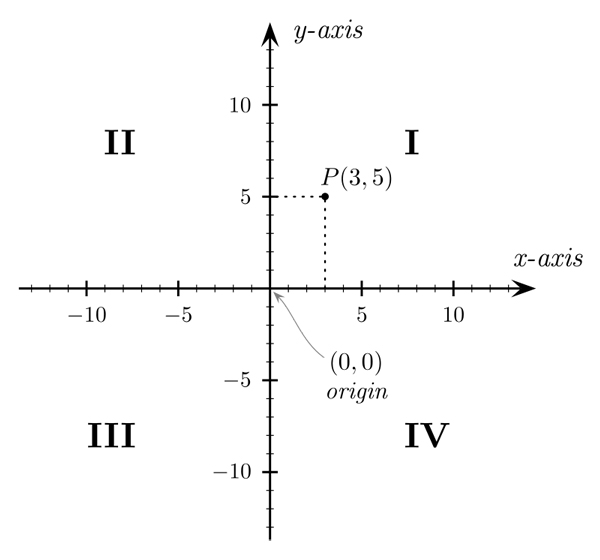
→ สิ่งที่เดการ์ตคิดค้นสร้างขึ้นไม่ได้เป็นเพียงสูตรใดสูตรหนึ่งแต่เป็นวิชาเรขาคณิตวิเคราะห์ที่มีพื้นฐานจากการกำหนดตำแหน่งจุดบนระนาบคาร์ทีเซียนตามรูปข้างบน ซึ่งสามารถนำไปใช้ประโยชน์ได้อย่างมากมายมหาศาล เช่น การเขียนกราฟ ทำแผนที่ และวิเคราะห์การเคลื่อนที่ของวัตถุในทุกรูปแบบ รวมทั้งนำไปสู่การค้นพบวิชาแคลคูลัสและวิชาคณิตวิเคราะห์

8. กอทท์ฟรีด วิลเฮล์ม ไลบ์นิซ (Gottfried Wilhelm Leibniz)
กอทท์ฟรีด วิลเฮล์ม ไลบ์นิซ (ค.ศ. 1646 – 1716) เป็นนักปรัชญาและนักคณิตศาสตร์ชาวเยอรมันผู้เป็นพหูสูตคนหนึ่งของยุคนั้น เป็นเสาหลักของนักปรัชญากลุ่มเหตุผลนิยม (Rationalism) ร่วมกับเรอเน เดการ์ต ไลบ์นิซเป็นคนแรกที่ใช้คำว่า “ฟังก์ชัน” สำหรับอธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้งหรือจุดบนเส้นโค้ง เขายังเป็นผู้ริเริ่มใช้สัญลักษณ์และเครื่องหมายต่างๆในวิชาคณิตศาสตร์มากมาย ใช้วงเล็บในการแยกเทอมต่างๆในวิชาพีชคณิต ใช้จุดแสดงการคูณแทนเครื่องหมายคูณที่มักสับสนกับตัวอักษร x และใช้ ∫ แทนผลรวมด้วยมีลักษณะเหมือน s ซึ่งมาจากคำว่า sum การรู้จักใช้สัญลักษณ์ต่างๆที่กระชับรัดกุมและสื่อความหมายดีนี้มีผลให้ผลงานคณิตศาสตร์ในยุโรปก้าวหน้าอย่างรวดเร็ว แต่ผลงานที่สำคัญที่สุดของไลบ์นิซคือการคิดค้นพัฒนาวิชาแคลคูลัสซึ่งส่งผลให้เปลี่ยนโฉมของวิทยาศาสตร์ และทำให้วิทยาศาสตร์โดยเฉพาะฟิสิกส์เป็นวิชาที่ทรงพลังมาก เพราะสามารถใช้แคลคูลัสศึกษาปัญหาที่ยากและซับซ้อนจากการมีหลายตัวแปรได้ดี
ไลบ์นิซคิดวิธีหาพื้นที่โดยการรวมพื้นที่เล็กๆเข้าด้วยกันและหาปริมาตรโดยการรวมปริมาตรเล็กๆ รวมถึงการหาความยาวโดยการรวมความยาวท่อนสั้นๆ ไลบ์นิซเรียกเทคนิคเหล่านี้ว่า calculus และตีพิมพ์เป็นหนังสือในปี 1684 แต่ก่อนหน้านั้นไอแซก นิวตันได้คิดวิธีคำนวณเพื่อใช้แก้ปัญหากลศาสตร์ที่เกี่ยวกับการเคลื่อนที่ซึ่งเขาเรียกว่า fluxion ซึ่งเป็นเรื่องเดียวกับ calculus ของไลบ์นิซ เพียงแต่นิวตันไม่ได้ตีพิมพ์เป็นหนังสือ แต่ได้สอดแทรกทั้งทฤษฎีและการประยุกต์ใช้ไว้ในหนังสือหลายเล่มที่พิมพ์ก่อนปี 1684 นิวตันได้โจมตีไลบ์นิซว่าแอบขโมยความคิดของเขาไป แต่ไลบ์นิซได้ปฏิเสธอย่างแข็งขันและย้ำว่าไม่เคยเห็นหรืออ่านงาน fluxion ของนิวตันเลย เนื่องจากนิวตันเป็นนักวิทยาศาสตร์ผู้มีอิทธิพลมากที่สุดในโลก บรรดาเพื่อนฝูงและลูกศิษย์ต่างก็ออกมาสนับสนุนเขา ไลบ์นิซจึงถูกประนามและถูกเกลียดชังโดยคนอังกฤษทั้งประเทศ ทุกวันนี้นักประวัติศาสตร์คณิตศาสตร์ได้เห็นพ้องกันว่าไลบ์นิซและนิวตันสร้างแคลคูลัสขึ้นมาโดยไม่มีใครลอกเลียนใคร และนิวตันสร้างได้ก่อนไลบ์นิซประมาณ 10 ปี (แต่ไม่ตีพิมพ์) แต่สัญลักษณ์และเครื่องหมายของไลบ์นิซได้รับความนิยมมากกว่า นอกจากนี้ไลบ์นิซยังเป็นคนแรกที่ประดิษฐ์เครื่องคำนวณที่คูณ หาร และหารากที่สองได้ รวมทั้งเป็นผู้คิดค้นระบบเลขฐานสองซึ่งเป็นพื้นฐานการทำงานของคอมพิวเตอร์อีกด้วย
ผลงานเด่น :
– คิดค้นวิชาแคลคูลัส
– คิดค้นและริเริ่มใช้สัญลักษณ์และเครื่องหมายทางคณิตศาสตร์ที่สำคัญจำนวนมาก
– คิดค้นระบบเลขฐานสอง
สูตรเด็ด :
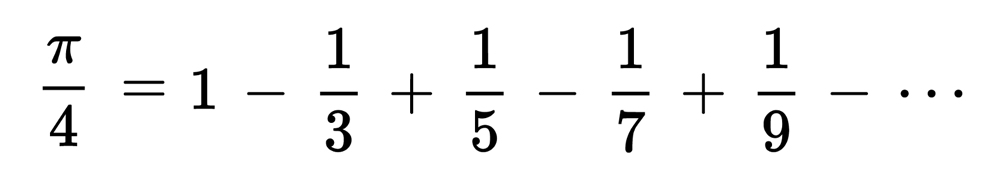
→ สูตรการหาค่า π (pi) มีการคิดค้นกันมามากมายนับพันสูตร สูตรของไลบ์นิซที่เรียกว่า Leibniz series นี้จัดว่าเป็นหนึ่งในสูตรหาค่า π ที่เข้าใจง่ายที่สุด

9. แบร์นฮาร์ด รีมันน์ (Bernhard Riemann)
แบร์นฮาร์ด รีมันน์ (ค.ศ. 1826 – 1866) เป็นนักคณิตศาสตร์ชาวเยอรมันผู้มีผลงานโดดเด่นในสาขาคณิตวิเคราะห์ ทฤษฎีจำนวน และเรขาคณิตเชิงอนุพันธ์ที่ไอน์สไตน์นำไปใช้ในการสร้างทฤษฎีสัมพัทธภาพทั่วไป รีมันน์เก่งคณิตศาสตร์ตั้งแต่เด็ก วิทยานิพนธ์ปริญญาเอกของเขาสร้างความประทับใจให้กับฟรีดริช เกาส์สุดยอดนักคณิตศาสตร์แห่งยุคมาก ถึงกับชื่นชมว่ามีคุณค่าสูงส่งเกินมาตรฐานของวิทยานิพนธ์ระดับปริญญาเอกเพราะผลงานนี้ได้ทำให้เกิดองค์ความรู้ใหม่มากมาย เช่น Riemann Surfaces, Theory of Holomorphic Functions, Topology, Algebraic Geometry และ Differential Geometry รีมันน์ทำงานเป็นอาจารย์สอนคณิตศาสตร์จนได้รับแต่งตั้งเป็นศาสตราจารย์ และได้รับแต่งตั้งเป็นสมาชิกต่างชาติของราชสมาคมแห่งลอนดอน (Royal Society of London) และสภาวิจัยวิทยาศาสตร์ของฝรั่งเศส (French Academy of Sciences)
รีมันน์ในวัย 33 ปีได้เสนอฟังก์ชันหนึ่งซึ่งมีโดเมนเป็นจำนวนเชิงซ้อนเรียกว่า Riemann zeta function และตั้งสมมุติฐานว่าคำตอบที่ทำให้ค่าของฟังก์ชันนี้เท่ากับศูนย์คือจำนวนเต็มคู่ลบ (-2, -4, -6, …) กับจำนวนเชิงซ้อนที่จะต้องมีส่วนจริง (real part) เท่ากับ ½ เท่านั้น จากปี ค.ศ. 1859 จนกระทั่งถึงทุกวันนี้ก็ยังไม่มีใครสามารถพิสูจน์สมมติฐานนี้ได้ โจทย์นี้จึงเป็นโจทย์คณิตศาสตร์ที่ยากที่สุดโจทย์หนึ่งของโลก ดาฟิด ฮิลแบร์ต (David Hilbert) นักคณิตศาสตร์ชื่อดังอีกคนหนึ่งถึงกับบอกว่าถ้าเขานอนหลับไปหลายศตวรรษแล้วตื่นขึ้นมา คำถามแรกที่เขาจะถามผู้คนรอบข้างคือมีใครพิสูจน์สมมติฐานของรีมันน์ (The Riemann Hypothesis) ได้แล้วบ้าง ถึงวันนี้ถ้าใครพิสูจน์สมมติฐานนี้ได้ว่าจริงหรือไม่จริง สถาบัน Clay Mathematics Institute ก็จะมอบเงินรางวัล 1 ล้านเหรียญให้แก่ผู้นั้น ปัจจุบันนักคณิตศาสตร์ได้พบว่าเทคนิคการวิเคราะห์สมมติฐานของรีมันน์ สามารถนำไปใช้ในการแก้ปัญหาอื่นๆได้อีกหลายเรื่อง เช่น Quantum Chaos, Cryptography และ Network Design น่าเสียดายที่รีมันน์อายุสั้นแค่เพียง 39 ปีมิฉะนั้นวิชาคณิตศาสตร์อาจมีความก้าวหน้ามากกว่านี้
ผลงานเด่น :
– ทฤษฎีฟังก์ชันตัวแปรเชิงซ้อน
– Riemann surface ซึ่งริเริ่มนำโทโพโลยีมาใช้ในวิชาคณิตวิเคราะห์
– พัฒนาแนวคิดเรื่องอินทิกรัลที่รู้จักดีในชื่อ Riemann integral
– พัฒนาเรขาคณิตเชิงอนุพันธ์
สูตรเด็ด :
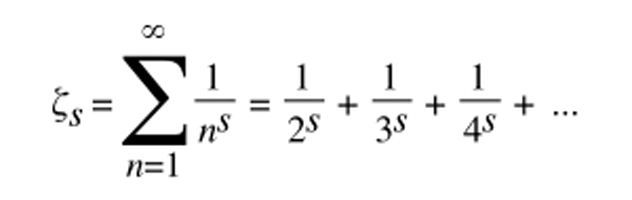
→ นี่คือสูตรของ Riemann zeta function ที่เกิดจากความประสงค์ของรีมันน์ที่ต้องการศึกษาเกี่ยวกับจำนวนเฉพาะซึ่งนำไปสู่สมมติฐานของรีมันน์อันโด่งดังที่ยังรอคอยคนเก่งมาพิสูจน์ความจริง

10. ปีแยร์ เดอ แฟร์มา (Pierre de Fermat)
ปีแยร์ เดอ แฟร์มา (ค.ศ. 1607 – 1665) มีอาชีพเป็นนักกฎหมายแต่ชอบศึกษาค้นคว้าคณิตศาสตร์ ได้รับการยอมรับว่าเป็นผู้พัฒนาทฤษฎีพื้นฐานที่นำไปสู่การค้นพบวิชาแคลคูลัส เขามีผลงานโดดเด่นในเรื่องทฤษฎีจำนวน เรขาคณิตวิเคราะห์ ความน่าจะเป็น รวมไปถึงเรื่องคุณสมบัติของแสง แฟร์มาริเริ่มบุกเบิกวิชาเรขาคณิตวิเคราะห์ในช่วงเวลาที่ใกล้เคียงกับเรอเน เดการ์ตผู้ได้รับการยกย่องว่าเป็นผู้สร้างวิชาเรขาคณิตวิเคราะห์ แฟร์มาเป็นผู้ค้นพบวิธีการต้นแบบของการหาจุดสูงสุด จุดต่ำสุด และเส้นสัมผัสของเส้นโค้งซึ่งคล้ายกับในวิชาแคลคูลัสเชิงอนุพันธ์ เขายังเป็นคนแรกที่หาค่าอินทิกรัลของฟังชั่นกำลัง วิธีการของเขาสามารถลดการหาค่าเป็นผลรวมของอนุกรมเรขาคณิต ทำให้ได้สูตรที่ช่วยให้ไอแซก นิวตันและกอทท์ฟรีด ไลบ์นิซพัฒนาวิชาแคลคูลัสได้สำเร็จ แต่สิ่งที่ทำให้แฟร์มามีชื่อเสียงโด่งดังทั่วโลกคือการเสนอทฤษฎีที่เรียกว่าทฤษฎีบทสุดท้ายของแฟร์มา
เนื่องจากแฟร์มาไม่ได้เป็นนักคณิตศาสตร์อาชีพจึงไม่คิดจะตีพิมพ์ผลงานวิจัยใดๆ แต่ชอบเขียนโจทย์และคำตอบในจดหมายแล้วส่งไปให้เพื่อนฝูงอ่าน หลังจากที่แฟร์มาเสียชีวิตทายาทจึงนำจดหมาย และเอกสารต่างๆออกเผยแพร่ ทำให้นักคณิตศาสตร์ทั้งโลกรู้จักทฤษฎีบทสุดท้ายของแฟร์มาที่เสนอว่า ถ้า x, y, z เป็นจำนวนเต็มที่มีค่ามากกว่า 0 (คือเลข 1, 2, 3, …) และ n เป็นจำนวนเต็มที่มีค่ามากกว่า 2 (คือเลข 3, 4, 5, 5,…) สมการ xn + yn = zn ไม่มีทางเป็นไปได้ หรืออาจกล่าวว่าไม่สามารถหาค่า x, y, z ที่สอดคล้องกับสมการได้ ไม่มีใครสามารถพิสูจน์ทฤษฎีนี้ได้เลยจนเวลาผ่านไปเป็นร้อยปี ยังมีผู้คนพยายามพิสูจน์ทฤษฎีนี้อยู่ ทำให้มีความตื่นตัวในการศึกษาคณิตศาสตร์กันอย่างกว้างขวาง ในที่สุดแอนดรูว์ ไวลส์ (Andrew Wiles) นักคณิตศาสตร์ชาวอังกฤษได้พิสูจน์ทฤษฎีบทนี้ได้สำเร็จหลังจากเวลาผ่านไป 357 ปี ส่งผลให้เขาเป็นผู้มีชื่อเสียงก้องโลกและได้รับรางวัลอาเบลซึ่งเปรียบเสมือนกับรางวัลโนเบลสาขาคณิตศาสตร์ นับว่าแฟร์มาเป็นนักคณิตศาสตร์สมัครเล่นที่ได้รับการยกย่องและมีชื่อเสียงมากที่สุด
ผลงานเด่น :
– พัฒนาทฤษฎีพื้นฐานที่นำไปสู่การค้นพบวิชาแคลคูลัส
– พัฒนาเรขาคณิตวิเคราะห์
– พัฒนาทฤษฎีความน่าจะเป็นร่วมกับปัสกาล
– ปรับปรุงทฤษฎีจำนวน
สูตรเด็ด :
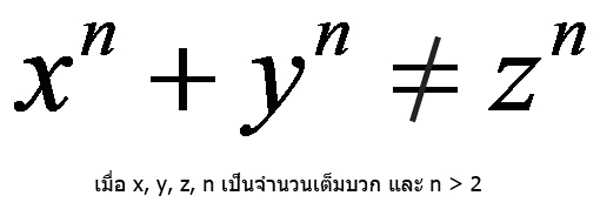
→ นี่คือหนึ่งในโจทย์คณิตศาสตร์ที่ยากที่สุดในประวัติศาสตร์ที่รู้จักกันในชื่อ “ทฤษฎีบทสุดท้ายของแฟร์มา” ที่ต้องใช้เวลา 357 ปีถึงจะมีคนพิสูจน์ได้สำเร็จ

ข้อมูลและภาพจาก elist10, wikipedia






