ปีแยร์ เดอ แฟร์มา (Pierre de Fermat) มีอาชีพเป็นนักกฎหมายแต่ชอบศึกษาค้นคว้าคณิตศาสตร์ ได้รับการยอมรับว่าเป็นผู้พัฒนาทฤษฎีพื้นฐานที่นำไปสู่การค้นพบวิชาแคลคูลัส นอกจากนี้เขายังมีผลงานโดดเด่นในเรื่องทฤษฎีจำนวน เรขาคณิตวิเคราะห์ ความน่าจะเป็น รวมไปถึงเรื่องคุณสมบัติของแสง แต่สิ่งที่ทำให้แฟร์มามีชื่อเสียงโด่งดังทั่วโลกคือการเสนอทฤษฎีที่เรียกว่าทฤษฎีบทสุดท้ายของแฟร์มาซึ่งได้กลายเป็นโจทย์คณิตศาสตร์ที่ยากที่สุดในโลกที่ต้องใช้เวลานานถึง 357 ปีกว่าจะมีคนที่สามารถพิสูจน์ทฤษฎีนี้ได้สำเร็จ แฟร์มาเป็นนักคณิตศาสตร์สมัครเล่นที่ได้รับการยกย่องว่าเก่งที่สุดและมีชื่อเสียงมากที่สุด
นักกฏหมายที่หลงใหลคณิตศาสตร์

ปีแยร์ เดอ แฟร์มา เป็นชาวฝรั่งเศส เกิดเมื่อปี 1607 ที่เมือง Beaumont-de-Lomagne ทางตอนใต้ของประเทศฝรั่งเศส พ่อของแฟร์มาเป็นพ่อค้าหนังสัตว์ที่มีฐานะร่ำรวยและยังเป็นกงสุลคนหนึ่งของเมือง Beaumont-de-Lomagne ด้วย ส่วนแม่ก็มาจากครอบครัวชนชั้นสูงดังนั้นเขาจึงได้รับการศึกษาเป็นอย่างดี และเขายังมีพรสวรรค์ด้านภาษาเป็นพิเศษสามารถพูดได้ถึง 6 ภาษาได้แก่ ฝรั่งเศส กรีก ละติน อิตาลี สเปน และอ็อกซิตัน ชีวิตและการศึกษาในวัยเด็กของเขาไม่มีข้อมูลชัดเจนแต่คาดว่าเขาน่าจะเรียนชั้นประถมและมัธยมที่โรงเรียนในแถบบ้านเกิด ปี 1623 แฟร์มาเข้าเรียนที่มหาวิทยาลัยออร์ลีนส์และจบระดับปริญญาตรีสาขากฏหมายเพ่งในปี 1626 ขณะมีอายุเพียง 18 ปี
หลังเรียนจบแฟร์มาไปทำงานเป็นทนายความอยู่ที่ศาลสูงของเมืองบอร์โดซ์อยู่หลายปีจนถึงปี 1630 เขาได้รับตำแหน่งสำคัญระดับสูงในศาลสูงแห่งเมืองตูลูสซึ่งทำให้เขากลายเป็นขุนนางสามารถใช้ชื่อ “ปีแยร์ เดอ แฟร์มา” แทนชื่อเดิมปีแยร์ แฟร์มาได้แล้ว และเขาได้ทำงานในตำแหน่งสำคัญนี้ไปตลอดชีวิต แฟร์มาแต่งงานกับ Louise de Long มีลูกด้วยกันหลายคนมีชีวิตอย่างปกติสุขแบบคนมีอันจะกินและนักกฎหมายที่ประสบความสำเร็จ แต่อาชีพนักกฎหมายของเขาไม่ได้ทำให้เขาเป็นที่รู้จักของคนทั่วไป กลับเป็นงานอดิเรกต่างหากที่ทำให้เขามีชื่อเสียงก้องโลก งานอดิเรกที่ว่าคือการศึกษาคณิตศาสตร์ แฟร์มาชื่นชอบหลงใหลและหมกมุ่นในคณิตศาสตร์เป็นอย่างมาก เขาเป็นนักคณิตศาสตร์สมัครเล่นที่ไม่เคยตีพิมพ์บทความใดๆเลย แต่ผลงานของเขากลับยิ่งใหญ่มากชนิดที่นักคณิตศาสตร์อาชีพยังเทียบไม่ติด
ปูพื้นฐานให้กับผู้คิดค้นวิชาแคลคูลัส
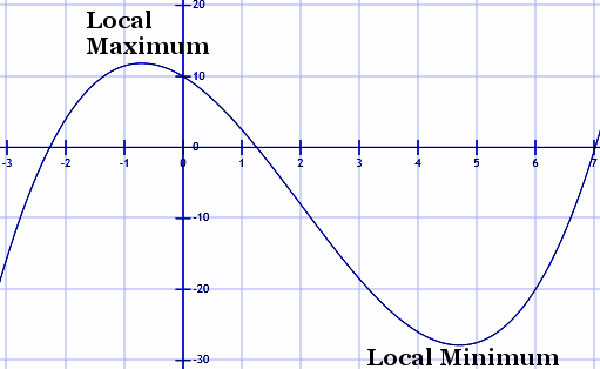
แฟร์มาไม่ใช่แค่เพียงหลงใหลในคณิตศาสตร์แต่เขาเป็นนักคณิตศาสตร์ที่เก่งกาจมาก เขาสนใจในคณิตศาสตร์ระดับสูงและศึกษาอย่างจริงจังขณะที่เขามีอายุ 19 ปีตอนที่เริ่มทำงานเป็นทนายความที่เมืองบอร์โดซ์ในปี 1627 เขามีเพื่อนสนิทที่เป็นเจ้าของห้องสมุดที่มีหนังสือสำคัญหลายเล่มและผลงานทางคณิตศาสตร์บางส่วนและนั่นคือจุดเริ่มต้น แฟร์มาให้ความสนใจเป็นพิเศษในผลงานของ Franciscus Vieta นักคณิตศาสตร์ชาวฝรั่งเศสที่ได้พัฒนาหลายอย่างเกี่ยวกับพีชคณิต รวมทั้งผลงานของนักคณิตศาสตร์ในยุคกรีกโบราณหลายคนโดยเฉพาะนักคณิตศาสตร์ผู้ยิ่งใหญ่อย่าง Archimedes จากการศึกษางานของ Vieta และ Archimedes (โดยเฉพาะในเรื่อง On Spirals) ทำให้แฟร์มาคิดค้นผลงานสำคัญชิ้นแรกคือวิธีใหม่ในการหาจุดสูงสุด จุดต่ำสุด และค่าแทนเจนต์ของเส้นโค้งอันเป็นพื้นฐานสำคัญที่ทำให้เกิดวิชาแคลคูลัส
แต่แฟร์มาเป็นแค่นักคณิตศาสตร์สมัครเล่นเขาไม่สนใจที่จะตีพิมพ์ผลงานที่เขาคิดค้นขึ้นนอกจากจะแลกเปลี่ยนความคิดทางคณิตศาสตร์กับเพื่อนของเขาผ่านทางการเขียนจดหมายถึงกัน เผอิญช่วงนั้นมีนักคณิตศาสตร์ชาวฝรั่งเศสชื่อ Marin Mersenne ที่พยายามส่งเสริมนักคณิตศาสตร์ให้มีการติดต่อสื่อสารกันอย่างกว้างขวางด้วยหวังว่ามันจะช่วยเร่งการพัฒนาด้านคณิตศาสตร์ ปี 1636 งานของแฟร์มาไปเข้าหู Mersenne เขาจึงติดต่อขอรายละเอียดแฟร์มาจึงส่งต้นฉบับเขียนด้วยมือของเขา 2 ชิ้นไปให้คือ Method for determining Maxima and Minima and Tangents for Curved Lines กับ Introduction to Plane and Solid Loci งานของแฟร์มาจึงถูกแจกจ่ายไปยังนักคณิตศาสตร์คนอื่นๆและไปปรากฏเป็นส่วนหนึ่งในผลงานของ Pierre Hérigone ที่ตีพิมพ์ในปี 1642
วิธีการหาจุดสูงสุด จุดต่ำสุด และค่าแทนเจนต์ของเส้นโค้งของแฟร์มาคล้ายกับในวิชาแคลคูลัสเชิงอนุพันธ์ เขายังเป็นคนแรกที่หาค่าอินทิกรัลของฟังชั่นกำลัง วิธีการของเขาสามารถลดการหาค่าเป็นผลรวมของอนุกรมเรขาคณิต ทำให้ได้สูตรที่มีส่วนช่วยให้ Isaac Newton และ Gottfried Leibniz พัฒนาวิชาแคลคูลัสได้สำเร็จ แต่เขาไม่ได้รับการยกย่องว่าเป็นผู้คิดค้นวิชาแคลคูลัสเพราะวิธีของเขาใช้ได้ผลในกรณีพิเศษเท่านั้น ไม่เหมือนกับของ Newton และ Leibniz ที่ใช้ได้ในทุกกรณี แต่อย่างไรก็ตามต้องถือว่าแฟร์มาคือบุคคลสำคัญที่อยู่เบื้องหลังการกำเนิดขึ้นของวิชาแคลคูลัส เพราะแม้แต่ Newton เองยังยอมรับว่าตอนที่เขาคิดค้นแคลคูลัส (ในช่วงทศวรรษ 1660) นั้นเขาได้แนวทางจากวิธีการวาดเส้นสัมผัส (Tangents) ของแฟร์มาที่เขาได้เห็นจากข้อเขียนเรื่อง Method for determining Maxima and Minima and Tangents for Curved Lines นั่นเอง
คิดค้นพัฒนาวิชาเรขาคณิตวิเคราะห์

ขณะที่ข้อเขียนแรกของแฟร์มาได้ปูพื้นฐานให้กับผู้คิดค้นวิชาแคลคูลัส แต่ในข้อเขียนที่สองเรื่อง Introduction to Plane and Solid Loci เป็นการคิดค้นพัฒนาคณิตศาสตร์สาขาใหม่ขึ้นมานั่นคือเรขาคณิตวิเคราะห์ (Analytic Geometry) โดยเขาได้แสดงให้เห็นว่าสมการจากพีชคณิตสามารถอธิบายหรือแปลงเป็นเส้นโค้งเรขาคณิตที่เท่าเทียมกันได้อย่างไร ต้นฉบับข้อเขียนของแฟร์มาถูกแจกจ่ายในหมู่นักคณิตศาสตร์ที่กรุงปารีสในช่วงปี 1636 – 1637 (แต่ไม่ได้ถูกตีพิมพ์ การตีพิมพ์ทำในปี 1679 หลังจากที่แฟร์มาเสียชีวิตไปแล้ว) ก่อนหน้าการตีพิมพ์หนังสือ Discourse on the Method ของ René Descartes ในปี 1637 เพียงเล็กน้อย หนังสือของ Descartes เล่มนี้เป็นผลงานที่มีอิทธิพลมากที่สุดชิ้นหนึ่งในประวัติศาสตร์ของปรัชญาสมัยใหม่ และในหนังสือเล่มนี้มีบทความชื่อ Geometry ที่เป็นจุดกำเนิดของวิชาเรขาคณิตวิเคราะห์เช่นกัน
วิชาเรขาคณิตวิเคราะห์จึงถูกคิดค้นขึ้นมาจากทั้งแฟร์มาและ Descartes อย่างเป็นอิสระในเวลาไล่เลี่ยกัน ความแตกต่างสำคัญในการพัฒนาเรขาคณิตวิเคราะห์ระหว่างแฟร์มาและ Descartes เป็นเรื่องของมุมมอง แฟร์มาจะเริ่มต้นด้วยสมการพีชคณิตก่อนเสมอจากนั้นจึงแปลงเป็นเส้นโค้งเรขาคณิตที่สอดคล้องกัน ในขณะที่ Descartes จะเริ่มต้นด้วยเส้นโค้งเรขาคณิตก่อนแล้วสร้างสมการพีชคณิตขึ้นในฐานะเป็นหนึ่งในคุณสมบัติหลายประการของเส้นโค้ง ด้วยเหตุนี้ Descartes จึงต้องจัดการกับสมการที่ซับซ้อนมากกว่าและเขาต้องพัฒนาวิธีการทำงานกับสมการพหุนามในระดับที่สูงขึ้น นี่อาจเป็นส่วนหนึ่งที่ทำให้ Descartes ได้รับเครดิตในฐานะผู้คิดค้นวิชาเรขาคณิตวิเคราะห์มากกว่า สังเกตได้จากระบบพิกัดฉากอันเป็นองค์ประกอบหลักในวิชาเรขาคณิตวิเคราะห์ถูกเรียกว่าระบบพิกัดคาร์ทีเซียน (Cartesian coordinate system) ซึ่งนำมาจากชื่อของ Descartes นั่นเอง
จากเกมพนันไปสู่วิชาความน่าจะเป็น

ในสมัยนั้นนักพนันนิยมเล่มเกมแห่งโอกาส (Game of chance) ที่ใช้อุปกรณ์ซึ่งให้ผลลัพธ์แบบสุ่มอย่างเช่น ลูกเต๋า รูเล็ต หรือเกมหยิบลูกบอลติดหมายเลขจากในกล่อง ในปี 1654 นักเขียนที่ชอบเล่นเกมพนันชาวฝรั่งเศสคนหนึ่งชื่อ Chevalier de Méré ได้หยิบยกปัญหาเชิงคณิตศาสตร์ที่มักเกิดขึ้นบนโต๊ะพนันขึ้นมาให้นักคณิตศาสตร์วิเคราะห์หาคำตอบคือในการเล่นเกมแห่งโอกาสที่กำหนดว่าผู้ชนะ 3 รอบก่อนเป็นผู้ได้เงินเดิมพัน สมมุติว่ามีผู้เล่น 2 คน A กับ B ลงเงินเดิมพันกันคนละ 32 เหรียญ เล่นไปแล้ว 3 รอบ A ชนะ 2 รอบ B ชนะ 1 รอบ แล้วเกิดเหตุมาขัดจังหวะไม่สามารถเล่นต่อไปได้ต้องหยุดไว้แค่นั้น คำถามคือจะแบ่งเงินเดิมพันอย่างไรจึงจะยุติธรรม
ปัญหานี้ถูกนำไปวิเคราะห์ร่วมกัน (ผ่านทางจดหมาย) ระหว่างแฟร์มากับ Blaise Pascal ผู้เป็นเพื่อนของ Chevalier de Méré แฟร์มาให้คำตอบในแง่ของโอกาสหรือความน่าจะเป็น เขาให้เหตุผลว่าเล่นกันอีก 2 รอบก็จะเพียงพอที่จะตัดสินชัยชนะได้ในทุกกรณี มีผลลัพธ์ที่เป็นไปได้ 4 แบบแต่ละแบบมีโอกาสเท่าเทียมกันคือ AA, AB, BA และ BB (หมายถึง A ชนะ 2 รอบ หรือ A ชนะจากนั้น B ชนะ หรือ B ชนะแล้ว A ชนะ หรือ B ชนะ 2 รอบ) จากผลลัพธ์ที่เป็นไปได้ 4 แบบนี้ 3 แบบแรกจะส่งผลให้ A เป็นผู้ชนะได้เดิมพัน มีเพียงแบบสุดท้ายแบบเดียวเท่านั้นที่จะส่งผลให้บีเป็นผู้ชนะได้เดิมพัน ดังนั้นอัตราต่อรองของ A : B คือ 3 : 1 การแบ่งเงินเดิมพันจึงสรุปได้ว่า A ควรได้ 48 เหรียญ ส่วน B ควรได้ 16 เหรียญ
Blaise Pascal ให้คำตอบในปัญหานี้แตกต่างออกไป เขาเสนอว่าพิจารณาการเล่นรอบต่อไปเพียงรอบเดียวก็ตัดสินได้แล้ว โดยสมมุติว่ารอบต่อไป B เป็นผู้ชนะซึ่งจะหมายความว่าผู้เล่นทั้งสองชนะสองรอบเท่ากันดังนั้นควรแบ่งเงินเดิมพันได้คนละ 32 เหรียญ แต่จริงๆแล้วโอกาสที่ B จะชนะในรอบต่อไปนั้นมีเพียงครึ่งเดียวดังนั้นเขาควรได้รับส่วนแบ่งเงินเดิมพัน 16 เหรียญ ส่วน A ควรได้รับ 32 + 16 = 48 เหรียญ แม้ว่าวิธีคิดของทั้งคู่จะแตกต่างกันแต่ได้คำตอบเดียวกันและนี่คือแนวคิดพื้นฐานของวิชาความน่าจะเป็น ต่อมา Christiaan Huygens นักวิทยาศาสตร์คนสำคัญชาวดัตช์เป็นผู้รวบรวมแนวคิดเรื่องความน่าจะเป็นอย่างเป็นระบบและตีพิมพ์เป็นบทความเรื่องทฤษฎีความน่าจะเป็นขึ้นเป็นครั้งแรกในปี 1657
หลายความก้าวหน้าในทฤษฎีจำนวน

สาขาคณิตศาสตร์ที่แฟร์มาศึกษามากที่สุดคือทฤษฎีจำนวน เขาได้รับแรงบันดาลใจและแนวคิดใหม่ๆจากหนังสือ Arithmetica ของนักคณิตศาสตร์ชาวกรีกโบราณ Diophantus ซึ่งตีพิมพ์เมื่อราวปี 250 ผลงานด้านทฤษฎีจำนวนของแฟร์มามีมากมายหลายเรื่อง ผลงานที่โดดเด่นส่วนหนึ่งมีดังนี้
Fermat’s two square theorem – ทุกจำนวนเฉพาะ p ที่อยู่ในรูป 4n + 1 สามารถแสดงในรูปผลบวกของจำนวนเต็มยกกำลังสองได้คู่หนึ่งและคู่เดียวเท่านั้นหรือเขียนในรูปสมการได้ดังนี้
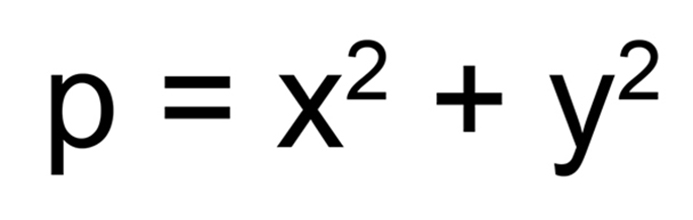
เมื่อ p เป็นจำนวนเฉพาะและ x, y เป็นจำนวนเต็ม
ตัวอย่างเช่น
4 (1) + 1 = 5 = 12 + 22
4 (3) + 1 = 13 = 22 + 32
4 (4) + 1 = 17 = 12 + 42
4 (7) + 1 = 29 = 22 + 52
4 (9) + 1 = 37 = 12 + 62
4 (10) + 1 = 41 = 42 + 52
Fermat numbers – แฟร์มาเป็นคนแรกที่ศึกษาตัวเลขที่ถูกเรียกว่า Fermat numbers ซึ่งเป็นจำนวนเต็มบวกที่อยู่ในรูป
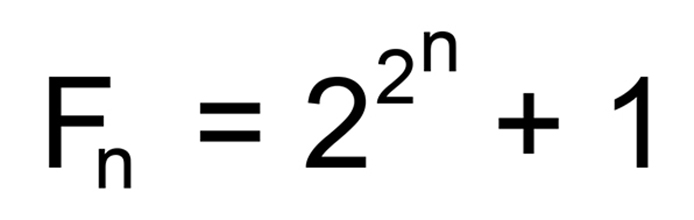
โดยที่ n เป็นจำนวนเต็มที่ไม่เป็นลบ (จำนวนเต็มบวกและ 0)
Fermat numbers ตัวแรกๆได้แก่ 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, … แฟร์มาคาดเดาว่า Fermat numbers ทุกตัวเป็นจำนวนเฉพาะ (และจำนวนเฉพาะที่เป็น Fermat numbers เรียกว่า Fermat primes) แต่ต่อมา Leonhard Euler ได้แสดงว่า Fermat numbers ตัวที่ 6 คือ 4294967297 ไม่เป็นจำนวนเฉพาะเพราะหารด้วย 641 ลงตัว และจนถึงปัจจุบัน Fermat primes ก็มีเพียง 5 ตัวคือ Fermat numbers 5 ตัวแรกเท่านั้น
Fermat’s little theorem – กล่าวว่าถ้า p เป็นจำนวนเฉพาะ สำหรับจำนวนเต็ม a ใดๆจะได้ว่า ap – a หารด้วย p ลงตัว เขียนเป็นสัญลักษณ์ในระบบเลขคณิตมอดุลาร์ได้ดังนี้
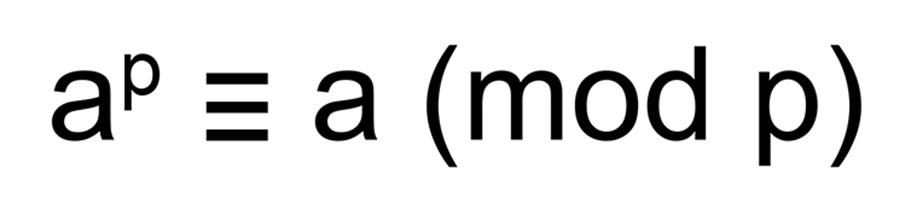
ตัวอย่างเช่น ถ้า a = 2 และ p = 7, ดังนั้น 27 = 128, และ 128 − 2 = 126 = 7 × 18 ซึ่งแสดงว่า 27 – 2 หารด้วย 7 ลงตัว
และถ้า a หารด้วย p ไม่ลงตัว จะได้ว่า ap − 1 − 1 หารด้วย p ลงตัว เขียนเป็นสัญลักษณ์ในระบบเลขคณิตมอดุลาร์ได้ดังนี้
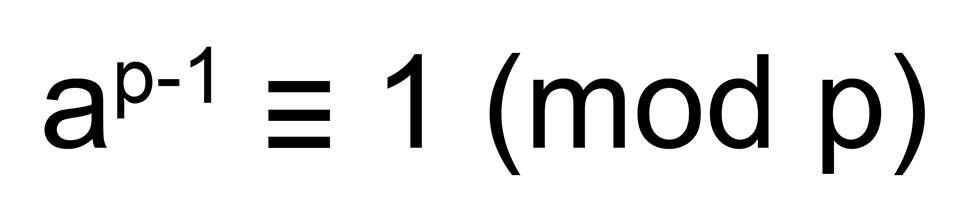
ตัวอย่างเช่น ถ้า a = 2 และ p = 7, ดังนั้น 26 = 64, และ 64 − 1 = 63 = 7 × 9 ซึ่งแสดงว่า 26 – 1 หารด้วย 7 ลงตัว
Fermat’s factorization method – หรือวิธีแยกตัวประกอบของแฟร์มานี้มาจากหลักการที่ว่า จำนวนเต็มคี่ใดๆสามารถแทนได้ด้วยผลต่างของเลขกำลังสองได้ดังนี้
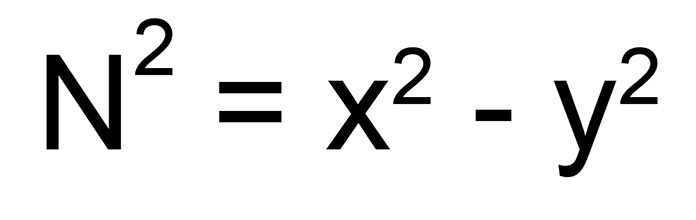
จากการสังเกตนี้ทำให้สามารถนำไปประยุกต์ในตะแกรงกำลังสอง (quadratic sieve) และวิธีแยกตัวประกอบของดิกสัน (Dixon’s Factorization Method) สำหรับใช้ในการแยกตัวประกอบจำนวนเต็ม วิธีแยกตัวประกอบของแฟร์มาเมื่อเทียบกับวิธีการหารเชิงทดลอง (trial division) อาจจะมีประสิทธิภาพน้อยกว่า แต่เมื่อนำสองวิธีมารวมกันแล้วจะทำให้ได้ประสิทธิภาพมากกว่าการใช้วิธีใดวิธีหนึ่ง
นอกจากนี้แฟร์มายังมีผลงานในเรื่องทฤษฎีจำนวนอีกหลายอย่าง เช่น Fermat’s right triangle theorem, Fermat polygonal number theorem, Fermat’s theorem (stationary points) เป็นต้น นับว่าผลงานของแฟร์มามีส่วนช่วยพัฒนาทฤษฎีจำนวนให้ก้าวหน้ามากยิ่งขึ้น แต่ผลงานและทฤษฎีทั้งหมดของแฟร์มายังไม่เป็นที่รู้จักมากเท่ากับผลงานอีกชิ้นหนึ่งซึ่งไม่มีใครรู้เลยนับจากที่เขาเขียนขึ้นไม่น้อยกว่า 30 ปีและมันถูกเผยแพร่หลังจากที่เขาเสียชีวิตไปแล้ว 5 ปี
ทฤษฎีบทสุดท้ายโจทย์ที่ยากที่สุด
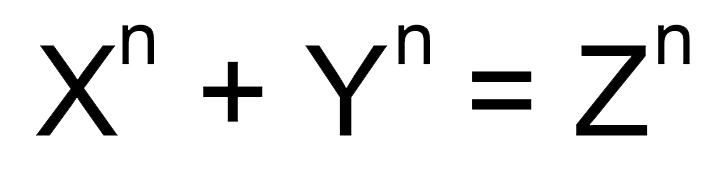
ปี 1651 เกิดโรคระบาดที่เมืองตูลูสแฟร์มาถูกรายงานว่าเสียชีวิตแต่เป็นรายงานที่ผิดพลาดเพราะเขารอดแม้ว่าเกือบไปเหมือนกัน เขามาเสียชีวิตจริงๆในปี 1665 มีอายุ 57 ปี เนื่องจากแฟร์มาปฏิเสธที่จะตีพิมพ์ผลงานเพื่อนๆของเขาจึงกลัวว่ามันจะถูกลืมในไม่ช้าเว้นแต่จะมีการทำอะไรบางอย่างเกี่ยวกับเรื่องนี้ Samuel ลูกชายของเขาจึงรับหน้าที่รวบรวมจดหมายของแฟร์มา รวมทั้งเอกสารทางคณิตศาสตร์และความคิดเห็นที่เขาเขียนไว้ในหนังสือ โดยมีวัตถุประสงค์เพื่อเผยแพร่แนวคิดทางคณิตศาสตร์ของพ่อ ต่อมา Samuel ก็ได้พบว่าพ่อของเขาได้เขียนข้อความหนึ่งบนที่ว่างในหน้าหนังสือ Arithmetica ของ Diophantus ที่เป็นหนังสือเล่มโปรดว่า “ฉันมีบทพิสูจน์ที่น่าอัศจรรย์สำหรับบทสรุปนี้ แต่พื้นที่กระดาษเหลือน้อยเกินไปที่จะอธิบายได้” และสิ่งที่เขาเขียนไว้เมื่อราวปี 1637 นี้ก็คือทฤษฎีบทสุดท้ายอันโด่งดังของเขานั่นเอง
ทฤษฎีบทสุดท้ายของแฟร์มา (Fermat’s last theorem) กล่าวว่า “ไม่มีจำนวนเต็มบวก x, y, และ z ที่ทำให้ xn + yn = zn เมื่อ n เป็นจำนวนเต็มที่มากกว่า 2″ ทฤษฎีบทสุดท้ายของแฟร์มาเป็นรูปแบบทั่วไปของสมการไดโอแฟนไทน์ (ตั้งชื่อเป็นเกียรติแก่ Diophantus) คือสมการ a2 + b2 = c2 เป็นสมการที่ตัวแปรเป็นจำนวนเต็มเท่านั้นซึ่ง Pythagoras เป็นคนแรกที่พิสูจน์ทฤษฎีนี้ได้ ชาวจีน ชาวกรีก และชาวบาบิโลเนียนได้ค้นพบคำตอบของสมการนี้หลายคำตอบ เช่น 3, 4, 5 (32 + 42 = 52) หรือ 5, 12, 13 เป็นต้น คำตอบเหล่านี้เรียกว่าสามจำนวนของพีทาโกรัส (Pythagorean triples) และมีอยู่จำนวนไม่จำกัด แต่ทฤษฎีบทสุดท้ายของแฟร์มากล่าวว่าสมการนี้จะไม่มีคำตอบเมื่อเลขยกกำลังมากกว่า 2 ทฤษฎีบทสุดท้ายของแฟร์มาดูแล้วเหมือนไม่มีอะไรซับซ้อนแต่กลับไม่มีใครสามารถพิสูจน์ได้ว่าจริงหรือไม่จริงจนเวลาผ่านไปเป็นร้อยปี มันจึงกลายเป็นโจทย์คณิตศาสตร์ที่ยากที่สุดโจทย์หนึ่งในประวัติศาสตร์
สำหรับตัวแฟร์มาเองมีหลักฐานว่าเขาสามารถพิสูจน์ทฤษฎีบทนี้ได้ในกรณี n = 4 ส่วนกรณี n = 3 ได้รับการพิสูจน์โดย Leonhard Euler และ Carl Friedrich Gauss เป็นผู้พิสูจน์ได้ในกรณี n = 5 แต่สำหรับกรณีทั่วไปหรือทุกกรณีนั้นไม่มีใครพิสูจน์สำเร็จ มีการตั้งรางวัลสำหรับผู้ที่พิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาสำเร็จหลายครั้ง ปี 1908 Paul Wolfskehl นักฟิสิกส์ผู้สนใจคณิตศาสตร์ชาวเยอรมันได้ทำพินัยกรรมมอบเงิน 100,000 โกลด์มาร์ก (เทียบเท่า 1 ล้านปอนด์ในปี 1997) ให้กับคนแรกที่พิสูจน์ทฤษฎีนี้สำเร็จ จนกระทั่งเวลาผ่านไปถึงปี 1993 Andrew Wiles นักคณิตศาสตร์ชาวอังกฤษผู้หลงใหลในทฤษฎีบทนี้มาตั้งแต่เด็กได้ใช้เวลา 7 ปีกับเครื่องมือทางคณิตศาสตร์หลายอย่างทำการพิสูจน์ทฤษฎีบทนี้สำเร็จแต่ในการนำเสนอครั้งแรกยังมีข้อบกพร่อง เขาจึงใช้เวลาอีก 1 ปีและด้วยความช่วยเหลือของ Richard Taylor ลูกศิษย์ของเขาเองบทพิสูจน์ฉบับสมบูรณ์จึงสำเร็จในปี 1994 ทำให้เขาได้รับรางวัล Abel Prize ซึ่งเปรียบเสมือนรางวัลโนเบลทางคณิตศาสตร์และได้รับการแต่งตั้งเป็นอัศวินอีกด้วย นับเป็นเวลานานถึง 357 ปีกว่าที่จะมีการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาสำเร็จ
นักคณิตศาสตร์สมัครเล่นที่เก่งที่สุด

แฟร์มาไม่ได้เก่งเฉพาะด้านคณิตศาสตร์เท่านั้นทางด้านฟิสิกส์เขาก็มีผลงานที่ยอดเยี่ยมอยู่เหมือนกันคือ Fermat’s Principle หรือ Principle of least time ที่กล่าวว่า “แสงเดินทางระหว่างจุดสองจุดตามเส้นทางที่ใช้เวลาน้อยที่สุด” ซึ่งสามารถนำมาใช้อธิบายการเดินทางเป็นเส้นตรงของแสง รวมถึงใช้พิสูจน์กฎการสะท้อนและกฎการหักเหของแสงได้ด้วย ผลงานที่โดดเด่นมากมายทางคณิตศาสตร์และฟิสิกส์ทำให้ผู้คนแทบจะลืมไปว่าเขามีอาชีพเป็นนักกฎหมาย การศึกษาคณิตศาสตร์เป็นแค่งานอดิเรกที่ทำในตอนที่มีเวลาว่างเท่านั้น แฟร์มาจึงได้รับการยกย่องว่าเป็นนักคณิตศาสตร์สมัครเล่นที่เก่งที่สุดและมีชื่อเสียงมากที่สุด

ข้อมูลและภาพจาก famousscientists, wikipedia, britannica